函数公式大全及图解-数学与工程应用指南

在数学和工程领域中，掌握各种函数公式是至关重要的。本文将为您详细解析函数公式大全，并通过图解的方式帮助您更好地理解和应用这些函数。

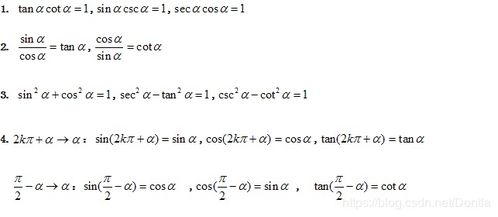
一、基础函数公式介绍

函数是数学中表达两个变量之间关系的一种方式。以下是一些基础的函数公式介绍：

1. 线性函数公式：y = mx + b（m代表斜率，b代表y轴截距）

2. 二次函数公式：y = ax^2 + bx + c（a、b、c为常数，a≠0）

3. 指数函数公式：y = e^x（e为自然对数的底数）

这些公式是函数学习的基础，也是进一步理解更复杂函数的前提。

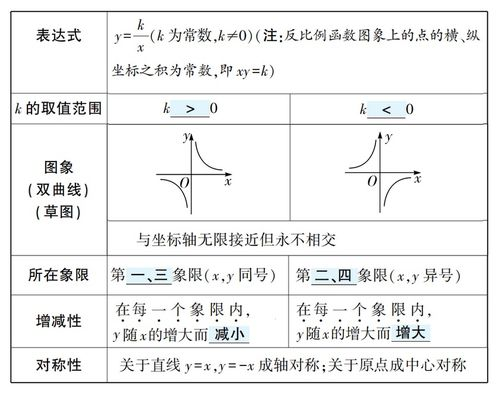
二、函数图像的理解

通过图像可以直观地理解函数的行为。，线性函数的图像是一条直线，二次函数的图像是一个抛物线，而指数函数的图像则是一个快速增长的曲线。

理解这些图像有助于预测函数在不同输入值下的输出值，以及函数的增减性。

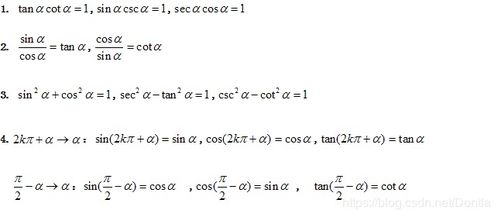
三、高级函数公式应用

在工程和科学研究中，经常使用到更复杂的函数公式，如：

1. 三角函数公式：sin(x
), cos(x
), tan(x)等

2. 对数函数公式：y = log(x)（以10为底的对数）

3. 双曲函数公式：sinh(x
), cosh(x
), tanh(x)等

这些函数在解决实际问题中扮演着重要角色。

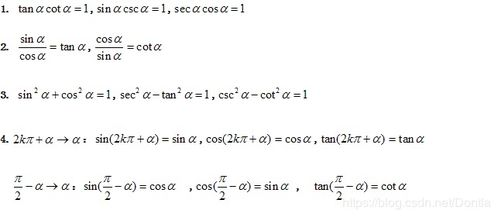
四、函数公式的实际应用

函数公式不仅在理论上重要，实际应用也非常广泛。，在物理学中，速度和加速度可以用函数公式表示；在经济学中，成本和收益也可以用函数公式来描述。

了解这些应用可以帮助我们更好地理解函数公式的实际意义。

五、函数图解技巧

绘制函数图像是理解函数行为的关键。通过使用计算软件或手动绘制，我们可以观察到函数的极值点、拐点等特征。

掌握图解技巧可以让我们更深入地理解函数的性质。

六、函数公式学习资源

网络上有大量的函数公式学习资源，包括在线课程、教科书和软件工具。合理利用这些资源可以加速学习过程。

，使用图形计算器或在线图形工具可以帮助我们更直观地理解函数图像。

函数公式是数学和工程领域中不可或缺的工具。通过本文的解析和图解，希望您能对这些公式有更深入的理解，并在实际应用中更加得心应手。