三角函数公式大全与应用解析

三角函数是数学中一个重要的分支，它在工程、物理学、计算机科学等领域有着广泛的应用。本文将为您详细解析三角函数公式大全，帮助您更好地理解和掌握这些关键公式。

一、基础三角函数公式

三角函数主要包括正弦（sin）、余弦（cos）、正切（tan）等基本函数。以下是一些基础的三角函数公式：

sin(θ) = 对边 / 斜边，cos(θ) = 邻边 / 斜边，tan(θ) = 对边 / 邻边。这些公式是三角函数计算的基础。

，在直角三角形中，若对边长度为3，斜边长度为5，那么sin(θ) = 3/5。

扩展词：三角函数计算、直角三角形、基础公式

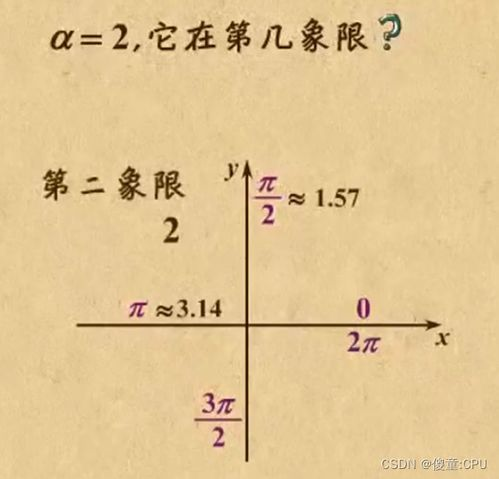
二、角度与弧度转换公式

在数学中，角度和弧度是两种表示角度大小的单位。它们之间的转换公式为：1弧度 = 180/π度，1度 = π/180弧度。这个公式在处理角度与弧度的转换时非常重要。

，90度等于π/2弧度，而π弧度等于180度。

扩展词：角度转换、弧度转换、单位换算

三、三角恒等式

三角恒等式是三角函数中的一些基本恒等关系，它们在求解复杂问题时非常有用。，sin²(θ) + cos²(θ) = 1，tan²(θ) + 1 = sec²(θ)。这些恒等式能够帮助我们简化问题。

，在求解三角函数方程时，利用这些恒等式可以减少计算量。

扩展词：三角恒等式、简化计算、方程求解

四、和差公式

和差公式用于计算两个角度的正弦、余弦和正切函数的和或差。，sin(α + β) = sin(α)cos(β) + cos(α)sin(β)，cos(α + β) = cos(α)cos(β) - sin(α)sin(β)。这些公式在解决角度变换问题时非常有用。

，在计算两个角度的正弦和时，使用和差公式可以简化计算过程。

扩展词：和差公式、角度变换、函数计算

五、倍角公式

倍角公式是用于计算角度的倍数的三角函数值。，sin(2θ) = 2sin(θ)cos(θ)，cos(2θ) = cos²(θ) - sin²(θ)。这些公式在求解涉及角度倍数的问题时非常重要。

，在求解cos(2θ)的值时，可以使用倍角公式cos(2θ) = 2cos²(θ) - 1。

扩展词：倍角公式、角度倍数、函数求解

六、反三角函数公式

反三角函数是三角函数的逆运算，包括反正弦（arcsin）、反余弦（arccos）和反正切（arctan）。反三角函数的公式可以帮助我们求解角度的值。

，若sin(θ) = 1/2，则θ = arcsin(1/2) = 30度。

扩展词：反三角函数、角度求解、逆运算

通过对三角函数公式大全的深入了解，我们能够更好地解决涉及三角函数的各种数学问题。无论是在学术研究还是实际应用中，这些公式都是不可或缺的工具。