三角函数公式大全,实用表格解析与应用指南

三角函数是数学中重要的基础概念，广泛应用于工程、物理、计算机科学等领域。以下是一篇关于三角函数公式大全的表格的文章，旨在帮助读者快速理解和记忆这些重要的数学工具。

一、三角函数的基本定义与性质

三角函数主要包括正弦（sin）、余弦（cos）、正切（tan）等，它们是基于直角三角形的边长比例或单位圆上的坐标定义的。以下是一些基本定义和性质：

- 正弦（sin）：对边与斜边的比值。

- 余弦（cos）：邻边与斜边的比值。

- 正切（tan）：对边与邻边的比值。

这些函数在不同角度下有不同的值，以下是常用的角度与对应函数值表格。

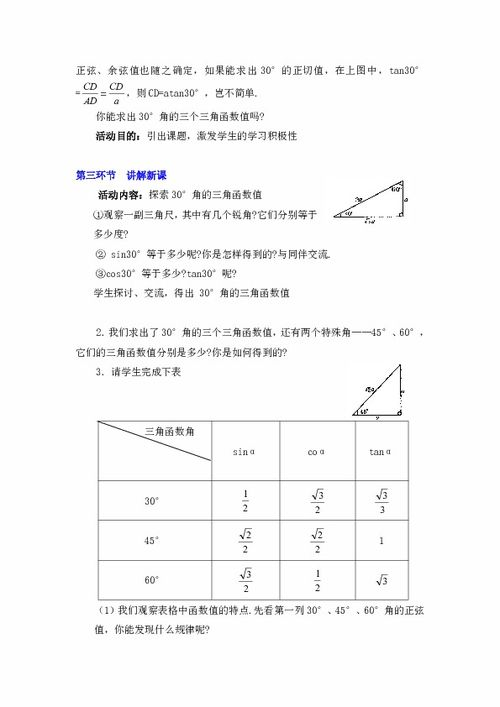
二、常用角度的三角函数值

以下是0°到90°之间常用角度的三角函数值：

角度 | sin | cos | tan
0° | 0 | 1 | 0
30° | 1/2 | √3/2 | 1/√3
45° | √2/2 | √2/2 | 1
60° | √3/2 | 1/2 | √3
90° | 1 | 0 | 无穷大

三、三角函数公式表格

以下是一些常见的三角函数公式，这些公式在解题中经常使用：

- 和差公式：sin(a ± b) = sin(a)cos(b) ± cos(a)sin(b)

- 积公式：sin(a)cos(b) = 1/2[ sin(a + b) + sin(a - b) ]

- 双角公式：sin(2a) = 2sin(a)cos(a)

- 半角公式：sin(a/2) = ±√[(1 - cos(a))/2]

四、三角函数的图像与变换

三角函数的图像是周期性的波形，了解其图像和变换对于解决实际问题非常重要。，y = A sin(Bx + C) + D 表示正弦函数的振幅、周期、相位和垂直位移的变换。

这些变换可以帮助我们理解和预测物理现象，如波动和振动。

五、三角函数在现实中的应用

三角函数在现实世界中有着广泛的应用，包括但不限于：

- 工程设计：在建筑、机械和电子工程中，三角函数用于计算角度、力的大小和方向。

- 物理科学：在声波、电磁波和量子力学中，三角函数描述波的形状和传播。

- 计算机图形：在游戏开发和动画制作中，三角函数用于创建平滑的运动和旋转。

三角函数公式表格是学习和应用三角函数的重要工具。通过理解和掌握这些公式，我们能够更好地解决实际问题，并在各个领域取得突破。